Differentiable Vietoris-Rips persistent homology¶
In this example, we essentially reproduce the toy experiment from
Notation¶
\(S\) is a mini-batch of points \(x \in \mathbb{R}^2\) of size \(|S|=b\)
\(\dagger(S)\) is the set of death-times obtained from the VR PH of \(S\)
\(\eta\) is the desired lifetime value (in our case \(\eta=2\))
\(\varepsilon_t, t \in \dagger(S)\) are the pairwise distance values of points in \(S\)
Learning task¶
Given a 2D point cloud (sampled from three Gaussians), find a mapping \(f_\theta: \mathbb{R}^2 \to \mathbb{R}^2\) (implemented via a simple MLP) such that the connectivity loss
is minimized over mini-batches of samples (\(S\)).
[1]:
%load_ext autoreload
%autoreload 2
[2]:
# PyTorch imports
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
from torch.utils.data.dataset import Subset, random_split, TensorDataset
# matplotlib imports
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
# misc
from collections import defaultdict, Counter
from itertools import combinations
# imports from torchph
from torchph.pershom import vr_persistence_l1
def apply_model(model, dataset, batch_size=100, device='cpu'):
"""
Utility function which applies ``model`` to ``dataset``.
"""
dl = torch.utils.data.DataLoader(
dataset,
batch_size=batch_size,
num_workers=0
)
X, Y = [], []
model.eval()
model.to(device)
with torch.no_grad():
for x, y in dl:
x = x.to(device)
x = model(x)
# If the model returns more than one tensor, e.g., encoder of an
# autoencoder model, take the first one as output...
if isinstance(x, (tuple, list)):
x = x[0]
X += x.cpu().tolist()
Y += (y.tolist())
return X, Y
# Run everything on the GPU
device = "cuda"
Toy data¶
First, we create a toy dataset with 2D points sampled from three Gaussians with different means and covariances. In particular, we create a class which derives from torch.utils.data.Dataset so we can later conveniently use PyTorch’s dataloader.
[3]:
class Toy2DData(torch.utils.data.Dataset):
def __init__(self, n_samples_by_class):
super().__init__()
X = []
Y = []
self.mus = [
[4.0,4.0],
[3.0,3.0],
[0.0,0.5]
]
self.sigmas = [
[1.0,1.0],
[3.0,3.0],
[0.5,0.5]
]
for y, (m, s) in enumerate(zip(self.mus, self.sigmas)):
X_class = torch.randn((n_samples_by_class, 2))* torch.tensor(s) - torch.tensor(m)
X.append(X_class)
Y += n_samples_by_class*[0]
self.X = torch.cat(X, dim=0)
self.Y = Y
def __len__(self):
return len(self.Y)
def __getitem__(self, item):
return self.X[item], self.Y[item]
def __iter__(self):
return zip(self.X, self.Y)
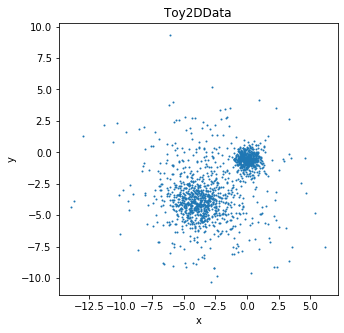
Let’s sample 1,500 points from this dataset (500 per Gaussian) and visualize the configuration in \(\mathbb{R}^2\).
[4]:
dataset = Toy2DData(500)
plt.figure(figsize=(5,5))
X = dataset.X.numpy()
plt.plot(X[:,0],
X[:,1], '.',markersize=2);
plt.xlabel('x')
plt.ylabel('y')
plt.title('Toy2DData');
Model & Optimization¶
We implement our mapping \(f_\theta\) as a simple MLP with three linear layers, interleaved with LeakyReLU activations. For optimization we use ADAM. We run over 30 epochs with a learning rate of \(0.01\) and over 20 additional epochs with a learning rate of \(0.001\).
[5]:
model = nn.Sequential(
nn.Linear(2, 10),
nn.LeakyReLU(),
nn.Linear(10, 10),
nn.LeakyReLU(),
nn.Linear(10, 2)
).to(device)
opt = torch.optim.Adam(
model.parameters(),
lr=0.01)
dl = DataLoader(
dataset,
batch_size=50,
shuffle=True,
drop_last=True)
# Get the transformed points at initialization
transformed_pts = [apply_model(model, dataset, device=device)[0]]
iteration_loss = []
for epoch_i in range(1, 51):
epoch_loss = 0
model.train()
# Learning rate schedule
if epoch_i == 20:
for param_group in opt.param_groups:
param_group['lr'] = 0.001
if epoch_i == 40:
for param_group in opt.param_groups:
param_group['lr'] = 0.0001
# Iterate over batches
for x, _ in dl:
x = x.to(device)
# Compute f_\theta(S)
x_hat = model(x)
"""
Loss computation (for \eta=2):
(1) Compute VR persistent homology (0-dim)
(2) Get lifetime values
(3) Compute connectivity loss
Note that all barcode elements are of the form (0,\varepsilon_t)!
"""
loss = 0
pers = vr_persistence_l1(x_hat, 0, 0)[0][0] # VR PH computation
pers = pers[:, 1] # get lifetimes
loss = (pers - 2.0).abs().sum() #
# Track loss over iterations and epochs
iteration_loss.append(loss.item())
epoch_loss += loss.item()
# Zero-grad, backprop, update!
opt.zero_grad()
loss.backward()
opt.step()
print('Epoch: {:2d} | Loss: {:.2f}'.format(epoch_i, epoch_loss/len(dl)), end='\r')
x_hat, _ = apply_model(
model,
dataset,
device=device)
transformed_pts.append(x_hat)
Epoch: 50 | Loss: 37.76
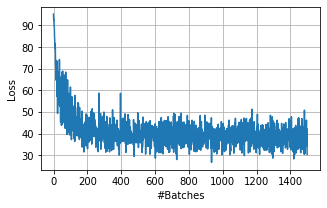
Visualize the loss over all iterations …
[6]:
plt.figure(figsize=(5,3))
plt.plot(iteration_loss)
plt.xlabel('#Batches');
plt.ylabel('Loss');
plt.grid();
Visualization¶
To study the effect of minimizing the connectivity loss, we freeze the model and check how the min/max/avg. lifetime changes over (1) epochs.
[7]:
def track_persistence_info(points, batch_size, N):
ds = TensorDataset(
torch.tensor(points),
torch.tensor([0]*len(points)))
dl = DataLoader(
ds,
batch_size=batch_size,
shuffle=True,
drop_last=True)
stats = defaultdict(list)
for i in range(N):
for x,_ in dl:
x = x.to(device)
pers = vr_persistence_l1(x, 0, 0)[0][0]
pers = pers[:, 1]
stats['alpha'].append(pers.min().item())
stats['beta'].append(pers.max().item())
stats['avgeps'].append(pers.mean().item())
return stats
[8]:
def visualize(transformed_pts, ax):
pts = np.array(transformed_pts)
x, y = pts[:,0], pts[:,1]
ax.plot(x, y, '.', **{'markersize':2, 'color':'black', 'alpha': 0.3})
stats = track_persistence_info(
pts,
50,
10)
ax.set_title(r'$\widehat{\alpha},\widehat{\varepsilon}, \widehat{\beta}$ = ' + '{:.2f}, {:.2f}, {:.2f}'.format(
np.mean(np.array(stats['alpha'])),
np.mean(np.array(stats['avgeps'])),
np.mean(np.array(stats['beta']))),
position=(0.04,0.02),
fontsize=12,
horizontalalignment='left',
bbox=dict(facecolor='white', alpha=0.7));
From left to right: Initialization (epoch 0), after 5 epochs, after 50 epochs:
[9]:
fig, axes = plt.subplots(1, 3, figsize=(14, 4))
for i, epoch in enumerate([0, 5, 50]):
ax = axes[i]
visualize(transformed_pts[epoch], ax)
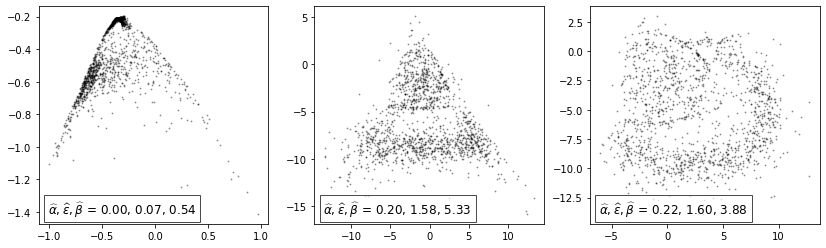
Note: Observe how the \([\hat{\alpha}, \hat{\beta}]\) interval gets tighter throughout the epochs and \(\hat{\varepsilon}\) gets closer to \(\eta=2\). However, arranging batches of size 50 in the desired manner is impossible in \(\mathbb{R}^2\) which is why the actual value of \(2\) is never reached (for details see paper).